Should you trust PyCO2SYS?¶
There are no "certified" results of marine carbonate system calculations against which software like PyCO2SYS can be unambiguously validated. But we can evaluate its performance by testing its internal consistency and by comparing its outputs with those from other programs.
PyCO2SYS v1.4.3+
All the comparisons, numbers and figures shown on this page were carried out with PyCO2SYS v1.4.3, and they apply equally to v1.5.
From v1.6.0, the comparisons with CO2SYS-MATLAB only apply to calculations with input pH on the Total scale. This is because a pH-scale conversion bug inherited from CO2SYS-MATLAB has now been fixed in PyCO2SYS.
Internal consistency¶
Round robin¶
PyCO2SYS can solve the marine carbonate system from any valid pair of total alkalinity, dissolved inorganic carbon, pH, partial pressure or fugacity or molinity of aqueous CO2, bicarbonate ion molinity, and carbonate ion molinity. In a "round robin" test, we first determine all of these core variables from one given input pair, and then solve the system again from the results using every possible combination of pairs as the input. We expect to find exactly the same results from every input pair combination.
Internal consistency of PyCO2SYS
- The differences arising from using different input pair combinations for the same composition are negligible.
- Any differences are at least 1010 times smaller than the best measurement accuracy for any of the variables.
We can conveniently run a round-robin test with PyCO2SYS for any given set of input conditions using PyCO2SYS.test.roundrobin (script available here):
# Import PyCO2SYS
import PyCO2SYS as pyco2
# Define test conditions
par1 = 2300 # parameter 1, here total alkalinity in μmol/kg-sw
par2 = 8.1 # parameter 2, here pH on the Total scale
par1type = 1 # "parameter 1 is total alkalinity"
par2type = 3 # "parameter 2 is pH"
sal = 33 # practical salinity
temp = 22 # temperature in °C
pres = 1000 # pressure in dbar
si = 10 # total silicate in μmol/kg-sw
phos = 1 # total phosphate in μmol/kg-sw
nh3 = 2 # total ammonia in μmol/kg-sw
h2s = 3 # total sulfide in μmol/kg-sw
pHscale = 1 # "input pH is on the Total scale"
k1k2c = 10 # "use LDK00 constants for carbonic acid dissociation"
kso4c = 3 # "use D90a for bisulfate dissociation & LKB10 for borate:sal"
# Run the test
res, diff = pyco2.test.roundrobin(par1, par2, par1type, par2type,
sal, temp, pres, si, phos, pHscale, k1k2c, kso4c, NH3=nh3, H2S=h2s,
opt_buffers_mode=0)
Running the round-robin test with the inputs in the example code above gave the following maximum absolute differences across all input pair combinations:
| Carbonate system parameter | Mean result | Max. abs. diff. |
|---|---|---|
| Total alkalinity / μmol/kg-sw | 2300.0 | 9.09·10−13 |
| Dissolved inorganic carbon / μmol/kg-sw | 1982.2 | 4.55·10−13 |
| pH (Total scale) | 8.1 | 1.78·10−15 |
| pCO2 / μatm | 312.0 | 1.53·10−12 |
| fCO2 / μatm | 311.0 | 1.48·10−12 |
| Carbonate ion / μmol/kg-sw | 218.1 | 8.53·10−14 |
| Bicarbonate ion / μmol/kg-sw | 1754.5 | 6.82·10−13 |
| Aqueous CO2 / μmol/kg-sw | 9.6 | 4.80·10−14 |
The maximum absolute differences across all the different input pair combinations are negligible in this example, all at least ten orders of magnitude smaller than the accuracy with which any of these variables can be measured. The differences are not exactly zero because the iterative pH solvers stop once a certain tolerance threshold is reached. By default, this threshold is set1 at 10−8 (in pH units) in PyCO2SYS.
Buffer factors¶
PyCO2SYS offers two independent ways to evaluate the various buffer factors of the marine carbonate system: with explicit equations and by automatic differentation.
Independent approaches give the same results
Differences between buffer factors calculated with explicit equations and by automatic differentiation are negligible.
The "explicit" approach is taken by functions in PyCO2SYS.buffers.explicit. These use the equations for each buffer factor that have been reported in the literature, corrected for typographical errors where known. These functions typically only include the effects of carbonate, borate and water alkalinity on each buffer, because the other components of alkalinity complicate the equations but usually only make a small difference to the result.
The "automatic" approach is PyCO2SYS's default behaviour and is taken by the functions in PyCO2SYS.buffers. These functions calculate each buffer factor based on its definition as a derivative in the literature. The relevant derivative of the appropriate function from PyCO2SYS.solve.get is evaluated automatically by Autograd (M16). This has several advantages:
- If the function in
PyCO2SYS.solve.getis correct, then its derivatives are also accurate. - All equilibrating solutes accounted for in the main alkalinity equation are automatically included in all derivatives too (not just carbonate, borate and water).
Comparing the results of these two independent methods with each other therefore supports that both are being executed correctly. For example, under typical open ocean conditions2 and with zero nutrients:
| Revelle factor | ψ | γDIC | γAlk | βDIC | βAlk | ωDIC | ωAlk | Q | |
|---|---|---|---|---|---|---|---|---|---|
| Explicit | 13.3336 | 0.7714 | 0.1612 | −0.1821 | 0.1821 | −0.1901 | −0.2090 | 0.1990 | 1.1291 |
| Automatic | 13.3336 | 0.7714 | 0.1612 | −0.1821 | 0.1821 | −0.1901 | −0.2090 | 0.1990 | 1.1291 |
| Difference | 1.56·10−8 | −2.83·10−7 | 3.18·10−7 | −3.88·10−7 | 3.88·10−7 | −4.05·10−7 | −4.89·10−7 | 4.24·10−7 | 1.80·10−7 |
We consider these differences all small enough to be negligible.
Although explicit check values are not available, we can attempt to recreate figures from the literature to check the consistency of PyCO2SYS's calculations. For example, you can use buffers_ESM10.py to make a passable replicate of Fig. 2 of ESM10:
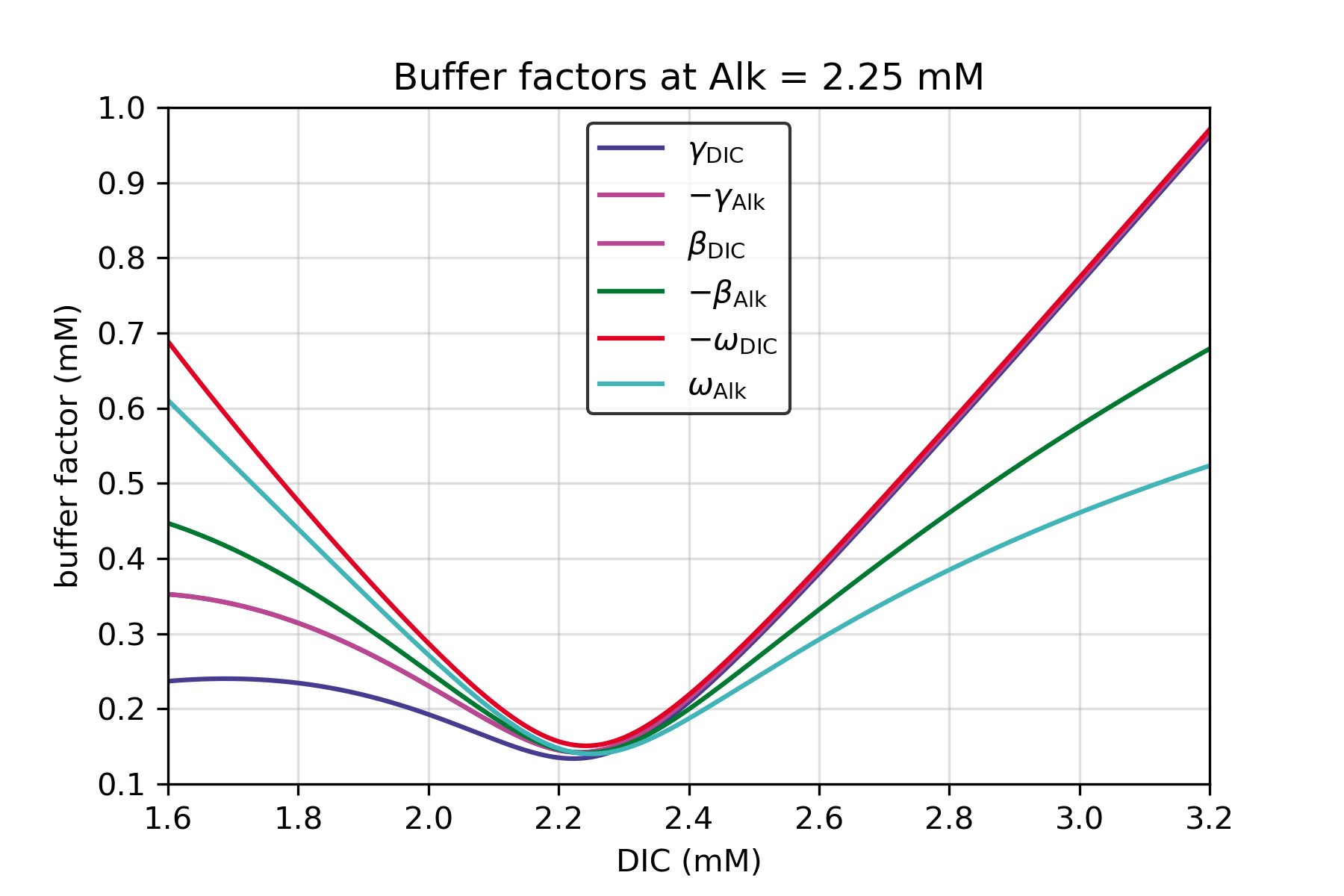
Switching between opt_buffers_mode=2 and opt_buffers_mode=1 in PyCO2SYS does not alter this figure sufficiently for any differences to be visible.
Uncertainty propagation¶
The uncertainty propagation calculations have been tested by comparing the directly calculated results with those of Monte-Carlo simulations (also conducted using PyCO2SYS). The tests have not identified any significant differences between these independent approaches.
You can see the tests that have been conducted, and run them for yourself, with the test scripts on GitHub.
External comparisons¶
CO2SYS for MATLAB¶
PyCO2SYS was originally based on CO2SYS for MATLAB, version 2.0.5. We should therefore expect that the results of these two programs will agree with each other perfectly, or that differences should be negligible for calculations where PyCO2SYS has since adjusted its calculation approach.
The MATLAB program has itself3 been rigorously compared with a suite of similar software packages that have been implemented in several different coding languages by OEG15. Indeed, it was used as the reference against which all other packages were compared, while noting that this does not guarantee it is error-free. Thanks to the work of OEG15, comparisons with CO2SYS for MATLAB allow us to assess the accuracy of PyCO2SYS in the context of all the software packages that they tested.
PyCO2SYS now calculates a wider array of properties than this version of CO2SYS for MATLAB, and it has more inputs and options, so not everything can be tested this way. However, some of the extra options can be tested against the new CO2SYS-MATLAB v3, available from GitHub.
What can and can't be compared?
Against CO2SYS v2.0.5 for MATLAB:
We cannot compare calculations with carbonate ion, bicarbonate ion or aqueous CO2 as one of the input marine carbonate system parameters, because these options are not available in CO2SYS v2.0.5 for MATLAB.
We also cannot test the PF87 input option for the hydrogen fluoride dissociation constant.
The PyCO2SYS outputs either not calculated or not returned by CO2SYS v2.0.5 for MATLAB are:
- All of the buffer factors except for the Revelle factor.
- All properties associated with NH3 and H2S.
- Total calcium molinity (although this is indirectly tested by the calcite/aragonite saturation state calculations).
Against CO2SYS v3 for MATLAB:
The new extended MATLAB version includes the full range of input marine carbonate system parameters, NH3 and H2S, and the PF87 input option for the hydrogen fluoride dissociation constant.
However, it still cannot be used to validate the buffer factors (again, except for the Revelle factor), nor directly the total calcium molinity.
Do it yourself
You can run the comparisons that the following discussion is based on yourself with:
compare_MATLABv2_0_5.m(in MATLAB) andcompare_MATLABv2_0_5.py(in Python) for MATLAB v2.0.5.compare_MATLAB_extd.mandcompare_MATLAB_extd.pyfor MATLAB v3.
The v3 results were generated using v3.0 of SPH20. You will need to download your own copy.
If you don't have a MATLAB license, you can run those scripts with the free and open source GNU Octave. Alternatively, the CSV files generated by the MATLAB scripts are available from GitHub.
In these tests, the marine carbonate system is solved from every possible combination of input parameter pair and CO2SYS settings, with non-zero nutrients and pressure. The results calculated by CO2SYS are then subtracted from those of PyCO2SYS for comparison.
PyCO2SYS vs CO2SYS-MATLAB
- Every variable computed by
PyCO2SYS.CO2SYSis negligibly different from its counterpart in CO2SYS v2.0.5 for MATLAB, except for the Revelle factor (see discussion below). - For CO2SYS-MATLAB v2.0.5, the absolute differences in all compared variables (except the Revelle factor) under the test conditions range from 0 to a maximum less than 10−6%.
- For CO2SYS-MATLAB v3, the absolute differences in all compared variables (except the Revelle factor) under the test conditions range from 0 to a maximum less than 10−3%.
- The difference between the MATLAB versions appears to be associated with sensitivity of the pH solvers from alkalinity and (bicarbonate) ions to the initial pH guess, which is different between the MATLAB and Python implementations. It is negligible for all practical purposes.
Nutrients not set to zero in MATLAB outputs
- Internally, both PyCO2SYS and CO2SYS-MATLAB set nutrients to zero for
K1K2CONSTANTSoptions6and8, and salinity too for8, because these variables should not be taken into account with these parameterisations. - These variables in the PyCO2SYS output
CO2dictare set to zero where appropriate (as of v1.4.0). This means that the values you see inCO2dictare those that were actually used in the calculations. - However, in MATLAB and in earlier versions of PyCOSYS, the outputs simply repeated the user inputs.
We've also compared the original CO2SYS clone in PyCO2SYS.original.CO2SYS against CO2SYS for MATLAB. It is important to remember that this module stands in isolation. It has its own self-contained set of functions for evaluating equilibrium constants and solving the marine carbonate system that do not interact with the rest of PyCO2SYS. Agreement between this module and CO2SYS for MATLAB tells us nothing about the performance of PyCO2SYS.CO2SYS or any of its underlying functions (and the opposite).
The original CO2SYS clone vs CO2SYS-MATLAB
- Every variable computed by the original CO2SYS clone in
PyCO2SYS.original.CO2SYSis virtually identical to its counterpart in CO2SYS v2.0.5 for MATLAB. - The absolute differences in all compared variables under the test conditions range from 0 to a maximum less than 10−9%.
Revelle factor discrepancy¶
Under the fairly typical open-ocean conditions used for these tests (for specifics, see the compare_MATLABv2_0_5 scripts), the maximum absolute differences between the Revelle factor under input and output conditions respectively were 0.09 and 0.11, which are almost 1% of the average calculated Revelle factor of ~12. While probably negligible in most real-world applications, these are too big to be acceptable from a software perspective.
Inconsistency between PyCO2SYS and CO2SYS-MATLAB
- The Revelle factor is about 1% different in PyCO2SYS compared with CO2SYS v2.0.5 for MATLAB.
- We understand why.
- The PyCO2SYS calculation is more accurate.
- The difference is probably too small to matter for most real-world applications of the Revelle factor.
There are three separate reasons for the difference, the first two of which could be considered as errors in CO2SYS for MATLAB:
- Incorrect reference DIC value used in the final evaluation.
- No "Peng correction" in calculation under output conditions.
- Relative inaccuracy of the finite-difference approach.
PyCO2SYS corrects errors 1 and 2 above. By default, PyCO2SYS also evaluates the Revelle factor using automatic differentiation, which is inherently more accurate.
With opt_buffers_mode=2, PyCO2SYS does use the finite-difference approach but it reduces the DIC perturbation size from 1 to 0.01 μmol/kg-sw to increase its accuracy. If we revert both this change and the corrections above, then PyCO2SYS returns Revelle factors that agree with CO2SYS for MATLAB to within 10−6%.
-
The pH tolerance threshold for all iterative solvers is controlled by
PyCO2SYS.solve.get.pH_tolerance. ↩ -
The default conditions for
PyCO2SYS.api.CO2SYS_wrapwith total alkalinity = 2300 μmol/kg-sw and DIC = 2150 μmol/kg-sw. ↩ -
The OEG15 intercomparison used CO2SYS v1.1 of HPR11, but the only difference between v2.0.5 and this in terms of solving the marine carbonate system is the addition of an extra set of carbonic acid dissociation constants. ↩